6.1 从全连接到卷积

要点

考虑一个图像，假设有百万像素，假设隐藏层是 100 个神经元，参数个数达到 $10^{6} \times 10^{2} = 10^{8}$ 个，这对训练来说是困难的，对于猫狗分类问题，都快赶上全部猫狗的数量，不如直接把所有猫狗记下来。

造成训练困难的原因是，全连接层过多的运用到像素间的信息，我们需要人为的给参数假定一些限制，保证学习可以进行下去

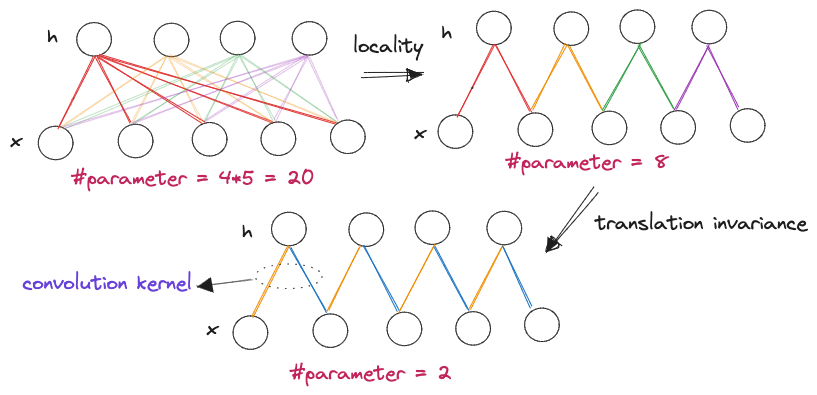卷积神经网络是简化版的全连接网络，参数个数大幅度减少

1. 重新考察全连接层

假设输入和输出都是矩阵，表示图像的宽度和高度，该单层神经网络输入的神经元是 $(h, w)$ 到 $(h^{'}, w^{'})$ ，权重是一个 4-D 的张量，其形状为 $(((h, w)), (h^{'}, w^{'}))$

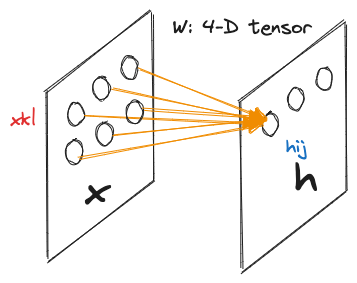一个图像的示意图

隐藏层任意单元可以计算为：

\begin{array}{r} \begin{aligned} {[H]}_{i, j} & = [U]_{i, j} + \sum_{k} \sum_{l} [W]_{i, j, k, l} [X]_{k, l} \\ = [U]_{i, j} + \sum_{a} \sum_{b} [V]_{i, j, a, b} [X]_{i + a, j + b} . \end{aligned} \end{array}

这里为了方便将张量 $W$ 进行重新索引，只需要满足 $k = i + a$ , $l = j + b$

这里和 [[3.7 softmax 回归简洁实现#^e19f0e]]不一样，这里不会将其展平，因为想利用图像的空间结构信息，展平会破坏这种空间结构

假设像素在 $X$ 中移动, 这种变换函数不应该随着像素点的位置进行变化（例如不管猫在图像的哪个位置，人都可以准确分辨出图像里的猫），也就是说 $[V]_{i, j, a, b} = [V]_{a, b}$ ，则有：

[H]_{i, j} = u + \sum_{a} \sum_{b} [V]_{a, b} [X]_{i + a, j + b} .

假设图像中有一只猫，人眼认识猫，只需要几个像素块就够了，不需要离猫很远的像素，也就说，影响 $h_{i j}$ 的只需要 $h_{i j}$ 附近的像素就够了，其余影响权重为 $0$ ：

[H]_{i, j} = u + \sum_{a = - Δ}^{Δ} \sum_{b = - Δ}^{Δ} [V]_{a, b} [X]_{i + a, j + b} .

上面 $V$ 表示一个卷积核